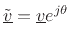Cauchy-Schwarz Inequality

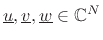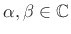The Cauchy-Schwarz Inequality (or ``Schwarz Inequality'') states that for all $ \underline{u}\in{\bf C}^N$ and $ \underline{v}\in{\bf C}^N$, we have
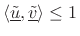$\displaystyle \zbox {\left\vert\left<\underline{u},\underline{v}\right>\right\vert \leq \Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert} $
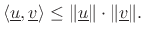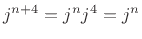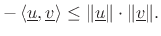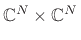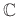with equality if and only if $ \underline{u}=c\underline{v}$ for some scalar $ c$. We can quickly show this for real vectors $ \underline{u}\in{\bf R}^N$, $ \underline{v}\in{\bf R}^N$, as follows: If either $ \underline{u}$ or $ \underline{v}$ is zero, the inequality holds (as equality). Assuming both are nonzero, let's scale them to unit-length by defining the normalized vectors 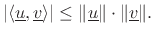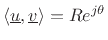$ \underline{\tilde{u}}\isdeftext \underline{u}/\Vert\underline{u}\Vert$, $ \underline{\tilde{v}}\isdeftext \underline{v}/\Vert\underline{v}\Vert$, which are unit-length vectors lying on the ``unit ball'' in 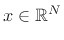$ {\bf R}^N$ (a hypersphere of radius 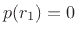$ 1$). We have

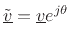
\begin{eqnarray*} 0 \leq \Vert\underline{\tilde{u}}-\underline{\tilde{v}}\Vert^2... ...=& 2 - 2\left<\underline{\tilde{u}},\underline{\tilde{v}}\right> \end{eqnarray*}
which implies
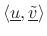$\displaystyle \left<\underline{\tilde{u}},\underline{\tilde{v}}\right> \leq 1 $
or, removing the normalization,
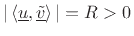$\displaystyle \left<\underline{u},\underline{v}\right> \leq \Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert. $
The same derivation holds if 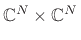$ \underline{u}$ is replaced by 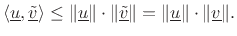$ -\underline{u}$ yielding
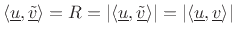$\displaystyle -\left<\underline{u},\underline{v}\right> \leq \Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert. $
The last two equations imply
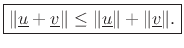$\displaystyle \left\vert\left<\underline{u},\underline{v}\right>\right\vert \leq \Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert. $
In the complex case, let 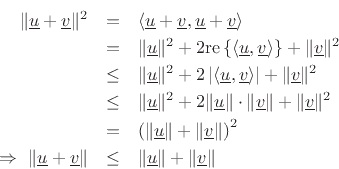$ \left<\underline{u},\underline{v}\right>=R e^{j\theta}$, and define 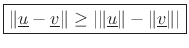$ \underline{\tilde{v}}=\underline{v}e^{j\theta}$. Then 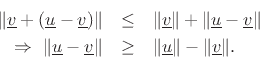$ \left<\underline{u},\underline{\tilde{v}}\right>$ is real and equal to 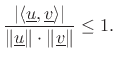$ \vert\left<\underline{u},\underline{\tilde{v}}\right>\vert=R>0$. By the same derivation as above,
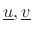$\displaystyle \left<\underline{u},\underline{\tilde{v}}\right>\leq\Vert\underli... ...derline{\tilde{v}}\Vert = \Vert\underline{u}\Vert\cdot\Vert\underline{v}\Vert. $
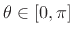Since $ \left<\underline{u},\underline{\tilde{v}}\right>=R=\left\vert\left<\underline{... ...right>\right\vert=\left\vert\left<\underline{u},\underline{v}\right>\right\vert$, the result is established also in the complex case.